【数学】確率の公式・解き方を完全解説！中学・高校の基礎から入試対策まで

確率は、数学における重要な分野の一つであり、特に入試問題でも頻出のテーマとなっております。
偶然に見える事象の中にも一定の法則性が存在し、それを数量的に捉えるのが確率の考え方です。
本コラムでは、受験に役立つ基礎的な知識から、典型問題の考え方までを丁寧に解説してまいります。

数学の確率とは？

数学における確率とは、ある出来事がどのくらい起こりやすいかを、数値で示したものです。
全ての結果の中で、目的の事象が起こる割合が確率となります。
値はゼロから一までの範囲にあり、一に近いほど起こりやすくなります。
確率を学ぶうえでは、試行、標本空間、事象といった基本的な概念を正しく理解することが重要です。

中学と高校での確率の違い

中学校では、主に基本的な確率の計算を学びます。
具体的には、サイコロやカードを用いた単純な事象について、「起こりうる場合の数」と「全体の場合の数」をもとに確率を求める方法が中心です。
一方、高校では、より抽象的で複雑な確率の考え方を学びます。
例えば、条件付き確率や独立な試行、場合の数との組み合わせ、確率分布など、論理的な思考力や数学的な構造の理解が求められます。
このように、高校では確率の概念がより体系的かつ発展的に扱われ、応用力が問われるようになります。

なぜ確率を学ぶことが重要なのか

確率は、様々な学問分野や実生活で活用される重要な概念です。
たとえば、天気予報、医療、経済、統計調査、AIの判断など、現代社会の多くの場面で確率の考え方が用いられています。
確率を学ぶことで、不確実な状況に対して論理的に判断し、より合理的な選択ができるようになります。
また、数学的な思考力や問題解決能力を養ううえでも、確率の理解は欠かせません。
したがって、確率を学ぶことは、単なる計算技術の習得にとどまらず、将来の多様な分野での活躍にもつながる重要な学びとなります。

確率学習で身につく思考

確率の学習を通じて身につく思考の一つは、物事を論理的に整理し、条件や前提を明確にしたうえで結論を導く力です。
確率の問題では、どのような条件のもとで何が起こりうるかを冷静に分析し、順序立てて考える必要があります。
また、複雑な状況を分解し、必要な情報を的確に見抜く力も養われます。
これにより、日常のさまざまな場面においても、感情に流されず、合理的な判断や選択ができる思考力が育まれます。
確率は、単なる計算ではなく、状況を読み解く力と筋道を立てて考える力を鍛える学問なのです。

中学数学で学ぶ確率の基礎知識

次に、中学数学でどのような確率の基礎知識を学ぶのか紹介していきます。

確率の基本公式

確率の基本公式は、ある事象が起こる確率を求める際の基本的な考え方を示しています。
確率は「目的の事象が起こる場合の数」を「すべての起こりうる場合の数」で割った値で表されます。
つまり、【確率 ＝ 目的の事象の起こる場合の数 ÷ 全ての可能な場合の数】となります。
この公式は、すべての結果が同様に起こりやすい（等確率）場合に成り立ちます。
例えば、サイコロを一つ投げて「3の目が出る確率」は、3の目が出る場合は1通り、全ての目は6通りなので、確率は1 ÷ 6となります。
この基本公式を理解し、正しく使うことが確率問題を解くうえで非常に重要です。

樹形図の書き方と活用法

樹形図は、複数の段階に分かれる場合の数を整理し、全ての結果をもれなく書き出すための手法です。
各段階の選択肢を枝分かれで表し、最後まで描き進めることで、全ての可能な結果を視覚的に確認できます。
これにより、複雑な場合の数を正確に数えられるだけでなく、確率を求める際にも計算ミスを防ぐことができます。
たとえば、硬貨を2回投げる場合、1回目の結果を「表」と「裏」に分け、それぞれから2回目の「表」と「裏」へと枝を伸ばします。
こうして全ての組み合わせを整理すると、「表・表」「表・裏」「裏・表」「裏・裏」の4通りがあることが一目でわかります。
樹形図は、条件付き確率や独立した複数の試行、さらには組み合わせや確率分布の理解にも役立ちます。
特に試行が複数段階に分かれる問題や、場合の数が複雑な問題で効果を発揮し、論理的に整理して問題解決に導く強力なツールとなります。

開始
/ \
表(H) 裏(T) ← 1回目の硬貨投げ
/ \ / \
表(H) 裏(T) 表(H) 裏(T) ← 2回目の硬貨投げ

枝の先端には、「HH」「HT」「TH」「TT」の4つの結果が並びます。
このように全ての結果を漏れなく書き出すことで、場合の数や確率を正確に求められます。

サイコロとコインの確率問題

①問題の内容を整理する。
まず、何をするのかをはっきりさせます。
例えば、「サイコロを1回投げる」「コインを2回投げる」など、試行の条件を確認します。

②すべての結果を考える。
サイコロの場合、出る目は1から6までの6通りです。
コインは表か裏の2通りです。
複数回の場合は、樹形図を使うと結果を漏れなく整理できます。

③求めたい事象を特定する。
問題で求められている事象がどのような結果を含むかを確認します。
例）サイコロで偶数の目が出る→2、4、6の3通り
コイン2回で表が1回だけ出る→「表・裏」「裏・表」の2通り

④確率を計算する。
確率は、目的の事象が起こる場合の数 ÷ 全ての結果の数で求めます。
たとえば、サイコロで偶数が出る確率は3割る6で1/2です。コインを2回投げて表が1回だけ出る確率は2÷4で1/2となります。
確率の問題は全ての場合の数を正確に数える事がカギとなります。
コインやサイコロの問題は表や目の出方を組み合わせで整理し、独立な試行は掛け算で考えましょう。

中学数学で頻出の確率問題パターン

【1】コインやサイコロの基本問題
例：サイコロを1回投げて「3の目が出る確率」
ポイント：全体の数と、条件に合う場合の数を数えて比を作る。

【2】複数回の試行（独立試行）
例：コインを2枚投げて「両方表が出る確率」
ポイント：全体の組合せは掛け算で計算する（2×2＝4通りなど）。

【3】条件付き確率
例：「1つは偶数が出ているとき、和が6になる確率」
ポイント：条件に合うケースだけを取り出して、その中でさらに求める。

【4】くじや袋からの取り出し（順番あり・なし）
例：袋に赤3個、白2個 → 2個同時に取り出して「両方赤」になる確率
ポイント：順番があるかどうかで数え方が変わる。基本は組合せ。

【5】数の性質に関する問題
例：1～20の整数から1つ選んで「3の倍数になる確率」
ポイント：条件に当てはまる数を数える（この場合、3,6,9,…18で6個）。

【6】表や樹形図を使って整理する問題
例：AさんとBさんがじゃんけんして、Aさんが勝つ確率
ポイント：すべての結果を漏れなく書き出して、条件に合うものを数える。

高校数学における確率の学習内容

次に高校数学ではどのような確率を学習するのかご紹介します。

順列・組合せと確率の関係

【順列】
順番を考えるときに使います。
たとえば、a・b・cの中から2人を選んで並べる場合、abとbaは違う並べ方になります。
3人から2人を並べて選ぶ方法の数は3 × 2 = 6通り（ab, ac, ba, bc, ca, cb）

【組合せ】
順番を考えないときに使います。
a・b・cから2人を選ぶとき、abとbaは同じ組み合わせになります。
組合せは「何通りの選び方があるか」だけを考えます。
よって、3人から2人を選ぶ場合 → ab, ac, bc の3通りとなります。
確率は「起こってほしい場合の数」 ÷ 「全部の場合の数」でもとめられます。
この「場合の数」を出すときに、順列か組合せを使います。

問題1(組み合わせ)
5人の中に女子が3人、男子が2人います。
この中から2人を選ぶとき、「2人とも女子」である確率は？
全ての選び方 → 5人から2人 → 組合せ：5×4÷2=10通り
女子だけから2人 → 3×2÷2=3通り
したがって確率は 3 ÷ 10 = 3/10となります。
問題2(順列)
6人から3人を選んで、並べてイスに座らせるとき、「1番前に男子が座る」確率は？

男子が2人、女子が4人とします。
全ての並べ方 → 6人から3人を選んで順に座らせる → 6×5×4 = 120通り
男子が1番前に座る → 男子2人から1人を選ぶ（1番前）→ 残り5人から2人を選んで並べる → 2×5×4 = 40通り
よって、確率は 40 ÷ 120 = 1/3となります。

独立試行と従属試行の違い

独立試行とは、一つの試行の結果が、他の試行の結果に左右されないような試行のことを指します。
独立試行ではそれぞれの事象の確率を掛け算します。
↳P(A かつ B)=P(A)×P(B)

例題）コインを2回投げて2回とも表が出る確率
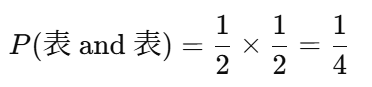従属試行とは、ある試行での結果が、次に行う試行の結果に影響を及ぼすような試行を指します。
従属試行では、条件付き確率を使って計算します。
P(A かつ B)=P(A)×P(B∣A)
（P(B∣A) はAが起きた後にBが起きる確率）

例題）5個の玉（赤2個、白3個）の入った袋から1個取り出し、戻さずにもう1個取り出す。2個とも赤玉の確率は？

まとめると、独立試行は、1回目の結果が2回目の確立に影響しない試行です。
従属試行は、1回目の結果が2回目以降の確率に影響を与える試行です。

条件付き確率の考え方と計算方法

条件付き確率とは、ある事象がすでに起こっていると仮定したうえで、別の事象が起こる確率を考えるものです。

公式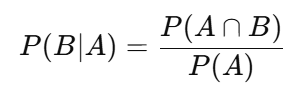：これは「Aが起きたときにBが起こる確率」です。

例題：袋の中に赤玉3個、白玉2個の計5個の玉が入っています。
1個玉を取り出して色を確認し、戻さずにもう1個取り出します。
最初に赤玉を引いたという条件のもとで、次も赤玉を引く確率を求めなさい。

【解き方】
一回目に赤玉を引く：

条件:一回目は赤だったとわかっている→袋の中は赤2個・白2個(計4個)になる。
その状態で赤を引く確率(条件付確率)：

【答え】
1回目に赤玉を引いたという条件の下で、2回目も赤玉を引く確率は　　１／2

確率変数と期待値

確率変数とは、確率的な事象に数値を対応させた変数のことです。
簡単に言うと、「試行の結果を数字で表したもの」です。
例：サイコロを1回振るとき、出る目を「確率変数 X」とする
X＝出た目Ｘ＝1,2,3,4,5,6

期待値とは、確率変数がとる値の平均（重み付き平均）です。
何回も試行したときに平均して得られる値を表します。
例：サイコロを1回振るときの出た目の期待値を求める。
確率変数 X=出た目　　各目（1～6）の確率は⅙

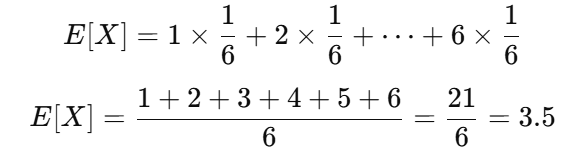
サイコロの出目の期待値は３．５

数学の確率計算のコツ

数学の確率計算のコツについて、ご紹介していきます。

「少なくとも」の問題を解くテクニック

例題として、「少なくとも1枚/回がAになる確率」を求める場合、
まず「全部Aにならない」を探し、次に確率を計算。
1からその確率を引く。という方法で解きます。

例：コインを３枚同時

樹形図を効率的に描くコツ

複雑な確率問題でも樹形図を効率的に描くためのコツを以下に解説します。
まず、問題文を注意深く読み込み、以下の点を明確にします。
試行の回数: 何回イベントが繰り返されるのか。
各試行の結果: 各試行でどのような結果が起こりうるのか。
各結果の確率: 各結果が生じる確率はいくらか（等しい場合もあれば、異なる場合もある）。
最終的に求めたい事象: 何の確率を計算したいのか。
樹形図の出発点となる最初の試行の結果を明確にします。
例えば、サイコロを振るなら「1の目」「2の目」…「6の目」、コインを投げるなら「表」「裏」などです。
それぞれの結果の横に、その確率を書き添えておくと後の計算が楽になります。
次に、各試行が前の試行の結果に影響されるのか（非独立試行）、されないのか（独立試行）を把握します。
独立試行の場合: 各分岐の確率は常に一定です。
非独立試行の場合（例：袋の中から玉を取り出す問題で、取り出した玉を戻さない場合）: 各分岐の確率は、前の試行の結果によって変化します。
この変化を正確に反映させることが重要です。
樹形図を視覚的に分かりやすく描くコツを説明します。
まず、同じ種類の事象には同じ記号を用いるなど、記号には一貫性を持たせます。
また、各分岐に「表」「裏」などと全て書くのではなく、T（表）、H（裏）のように頭文字を使うなど、簡潔に表記する工夫を凝らします。
そして各枝にその枝を通る確率を必ず記入します。
もし、樹形図が複雑になる場合は、以下の点を意識します。
対称性の利用: もし同じようなパターンが繰り返される場合、一部分だけ詳細に描き、他は「同様に」と省略したり、パターンに気づいて計算を簡略化できないか検討します。
不要な枝の省略: 最終的に求めたい事象に関係のない枝は、途中で描くのをやめる、または簡略化することを検討します。
例えば、「〇〇が起こらない場合」は詳細を省略するなどです。
グループ化: 特定の条件を満たす枝をグループとして認識し、そこまでの確率を一度計算してしまうことで、以降の計算を楽にすることができます。
全ての枝を描き終えたら、樹形図は完成です。
最終確認として、以下の点を確認するとミスが減るのでおすすめです。
全ての経路の確率の合計: 樹形図の最終的な経路（一番右端）の確率を全て合計すると、必ず1になるはずです。
これを確認することで、計算ミスや抜けがないかをチェックできます。
求めたい事象の経路の特定: 最終的に求めたい事象に対応する経路をすべて特定し、それらの確率を合計します。

場合分けの考え方

次に、場合分けの考え方について解説します。
場合分けとは、ある確率問題を、互いに重複せず、かつ全ての可能性を網羅するような複数の「場合（ケース）」に分割し、それぞれのケースについて独立に確率を計算し、最後にそれらの結果を統合する思考法です。
場合分けを適切に行うことで、複雑な確率問題をシンプルに分解し、一つひとつのケースを丁寧に検討することが可能になります。
これにより、見落としや重複を防ぎ、正確な答えにたどり着く確率が格段に向上します。
ここからは、確率計算で場合分けを効果的に行うための具体的なコツを説明します。
➀場合分けの「基準」を明確にする
最も重要なのは、どのような条件や性質に基づいて場合分けをするかを決めることです。
問題文の条件や、求めたい事象の性質をよく分析し、最も自然で分かりやすい基準を選びましょう。
・特定の結果の有無や回数
例：「少なくとも1回は表が出る確率」を求める際、「表が1回出る場合」「表が2回出る場合」「表が3回出る場合」のように、表が出る回数で場合分けする。
ただし、余事象も検討します。
上記の例では「全て裏が出る」という余事象を考えた方が計算が楽な場合が多いです。
場合分けと余事象は、どちらが効率的かを常に検討しましょう。
・試行の結果による分岐（状況の変化）
例：1回目に何が出たかによって、2回目以降の状況が変わる場合（例：袋から玉を取り出す問題で、取り出した玉を元に戻さない場合）。
・特定の要素の個数や状態
例：「カードを3枚引くときに、偶数が何枚含まれるか」で場合分けする（例：「偶数1枚、奇数2枚」「偶数2枚、奇数1枚」など）。
・変数の範囲や条件
例：ある変数が特定の値以上か未満かで確率の計算方法が変わる場合。
②各場合が「互いに排反」（重複しない）であることを確認する
分けた各ケースが同時に起こることがないように設定することが非常に重要です。
もし重複があると、その部分を二重に数えてしまい、正しい確率が得られません。
・悪い例: 「サイコロの目が偶数」と「サイコロの目が3の倍数」で場合分けする（6が重複する）。
・良い例: 例えば、「サイコロの目が1」「サイコロの目が2」「…」のように、完全に区別できる事象で分ける。
あるいは、「偶数で3の倍数でない」「奇数で3の倍数でない」「偶数で3の倍数である」「奇数で3の倍数である」といったように、網羅しつつ排反になるように細分化する。
③全ての可能性を「網羅」することを確認する
考えられる全てのケースを漏れなく考慮することが大切です。
一つでも抜けがあると、最終的な確率が不完全になります（合計しても1にならなかったり、明らかに答えが小さいなど）。
確認方法: 場合分けした各ケースの条件を全て合わせると、元の問題の全範囲がカバーされているかを確認します。
例えば、「〜以上」「〜未満」などの境界値の扱いにも注意し、どちらか一方に含めるなどして漏れがないようにします。
④最終的な確率を正しく「統合」する
各場合で計算した確率を、最後に適切に合計します。
多くの場合、排反な場合の確率は単純に足し合わせることで全体の確率が得られます。

数学の確率が苦手な人のための克服法

次に、数学の確率が苦手な人のための克服法について解説していきます。

確率が苦手な理由は把握する

まずは確率が苦手な理由や自分がどこでつまづいているのかを把握することが大切です。
苦手な理由は人により異なりますが、問題文の読解力不足や確率の概念理念が曖昧であったり、計算ミスなどが多いことが苦手な理由となりやすいです。
間違えた問題の解説をじっくり読み、どのステップでつまずいたか特定することが大事です。
「問題の意味が分からなかったのか」「公式の使い方が違ったのか」など、どこでつまずいたのか具体的にすることで、集中的に弱点を克服する学習計画が立てられます。
自分の弱点が分かれば、漠然とした「苦手」から脱却し、効率的に確率をマスターできます。

基礎からの積み上げて学習する

まず最初はやはり確率の基礎的な概念を固める必要があります。
基礎なくして応用問題を解くことはできません。
まずは基礎をしっかり固め、それから各問題に取り掛かりましょう。
次に例題を解いていきましょう。
このとき、いきなり難しいものを解くのではなく、教科書に載っているようなものから取り掛かりましょう。
基礎も例題も完璧にこなせるようになって初めて過去問や模擬試験の問題へ挑戦しましょう。
どんなものでも基礎、つまり土台が重要になってきます。基礎は怠らないようにしましょう。

視覚的に理解するための工夫

確率の問題は、目で見て理解する工夫をすれば、ぐっと分かりやすくなる分野です。
ここでは、図や表を使って確率を視覚的に捉える方法についてご紹介します。
確率の基本は、「起こりうるすべてのパターン」を理解することです。
これを視覚化するための最強ツールが樹形図（ツリー図）です。
例えば、「赤玉2個と白玉1個が入った袋から1個を取り出し、戻した後にもう一度1個を取り出す。」という文章があったとします。

条件整理：
・赤玉：2個　🔴🔴
・白玉：1個　⚪️
・玉は1回取り出したら戻す（元に戻る）

Step 1：1回目の取り出しを枝分かれで描く
まず、1回目に出る可能性は…
・赤が出る（確率：2/3）
・白が出る（確率：1/3）
であるので、以下のように描きます。

【1回目】
┌─ 赤（2/3）
スタート
└─ 白（1/3）

Step 2：2回目の結果もそれぞれに枝を伸ばす
玉は戻すので、2回目も同じ条件になります（赤2、白1のまま）。
よって、どちらから始まっても、2回目も赤か白の2通りに分かれます。

【1回目】 【2回目】
┌─ 赤 ─┬─ 赤
│ └─ 白
スタート
└─ 白 ─┬─ 赤
└─ 白

ここで、全部何通りあるかが視覚的にわかるようになります。

Step 3：確率をかけて求める
各ルート（枝）ごとに確率を計算します。

・赤→赤：2/3 × 2/3 = 4/9
・赤→白：2/3 × 1/3 = 2/9
・白→赤：1/3 × 2/3 = 2/9
・白→白：1/3 × 1/3 = 1/9

合計：4/9 + 2/9 + 2/9 + 1/9 = 1（全部の確率はちゃんと1になります！）

このように図にすると、全てのパターンが見えてきます。ここでのポイントは、文章のまま読まずに、図にして整理することです。

また、確率は「あるパターンが全体の中で何通りあるか」の割合を求めるものです。
よって、表を使って数を目で数えることがとても有効な手段となります。
例えば、サイコロ2個を同時に投げて、出た目の合計が偶数になる確率を求める場合、まずは表で全パターンを整理しましょう。

	①	②	③	④	⑤	⑥
①	2	3	4	5	6	7
②	3	4	5	6	7	8
③	4	5	6	7	8	9
④	5	6	7	8	9	10
⑤	6	7	8	9	10	11
⑥	7	8	9	10	11	12

偶数（2,4,6,8,10,12）のマスを数えると、18個であることが分かります。
全体は6×6=36通りであるため、答えは18÷36=1/2となります。

確率を学ぶときは、ただ式を追いかけるのではなく、目で見える地図を描く感覚を持つことが重要です。
道筋を示す樹形図やパターンを可視化する表などを活用して分かる感覚を身につけていきましょう。

医学部受験レベルの確率

最後に、医学部受験レベルの確率について解説していきます。

プロ講師による確率の解説

確率は、事象の起こる場合の数／起こりうる全ての場合の数として定義されます。
例えば、「ｎ人でじゃんけんをして、あいこになる確率」などですが、実際にこれを求めてみたいと思います。
まず、「あいこになる」ということは、「勝ちが決まらない」ということですので、

「あいこになる」⇔「勝ちが決まる」の余事象　⇔「ちょうど2種類」の余事象

となります。よって、「ちょうど2種類」になる場合の数を求めます。
「グー、チョキ」の2種類となるのは、2ⁿ-2 であり、「グー、パー」、「チョキ、パー」も同様に求められますので、結果は、3×(2ⁿ-2) となります。
そして全事象は 3ⁿ ですので、

あいこになる確率＝1-(2ⁿ-2)/3ⁿ⁻¹

となります。じゃんけんをする人数が増えれば増えるほど、なかなか勝負がつかなくなる、という感じです。
また、確率の定義では分母が有限集合となっていますので、無限集合では定義ができないのですが、直感的には、自然数から1つを選んだ時、それが偶数である確率が1/2、3の倍数である確率は1/3…という事も予測できます。
一般的に、p の倍数である確率は1/p である、とすると、これを繰り返し用いることで、

2つの自然数が互いに素になる確率＝6/n²

という事も示されます。証明には「素因数分解の一意性」などが使われます。

まとめ

本記事では、中学生から高校生まで幅広い学年の生徒に役立つ、確率の学習方法について基礎から丁寧に解説してきました。
特に、樹形図や表を使って全体の流れやパターンを整理する方法は、実践的かつ効果的です。
苦手意識を克服するための学習のコツや、基本的な計算の進め方も盛り込んでいますので、確率に自信がない方は、ぜひ繰り返し読み直して、自分の理解に落とし込んでみてください。